Identidades trigonometricas

En matemáticas, las identidades trigonométricas verificables para cualquier valor permisible de la variable o variables que se consideren (es decir, para cualquier valor que pudieran tomar los ángulos sobre los que se aplican las funciones).

Estas identidades, son útiles siempre que se precise simplificar expresiones que incluyen funciones trigonométricas. Otra aplicación importante es el cálculo de integrales indefinidas de funciones no-trigonométricas: se suele usar una regla de sustitución con una función trigonométrica, y se simplifica entonces la integral resultante usando identidades trigonométricas.

Notación: se define cos²α, sen²α, etc; tales que sen²α es (sen α)².

Relación pitagórica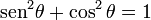
Identidad de la razón

Unidades angulares

En la medida de ángulos, y por tanto en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.

· Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.

· Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.

· Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.

Definicion de trigonometria

La trigonometría es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos.

La trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión.

Identidades trigonométricas 01